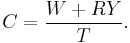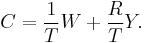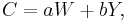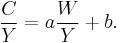Life-cycle hypothesis
The Life Cycle Hypothesis (LCH) is an economic concept analysing individual consumption patterns. The life-cycle hypothesis considers that individuals plan their consumption and savings behaviour over the long term and intend to even out their consumption in the best possible manner over their entire lifetimes. The key assumption is that all individuals choose to maintain stable lifestyles. This implies that they usually don't save up a lot in one period to spend furiously in the next period, but keep their consumption levels approximately the same in every period.
Contents |
Background
In the early 1950s, Franco Modigliani and his student, Richard Brumberg, developed a theory based on the observation that people make consumption decisions based on the resources available to them over their lifetime and which stage of life they are currently at. They had observed that individuals build up assets at the initial stages of their working lives. Later on during retirement, they make use of their stock of assets. The working people save up for their post-retirement lives and alter their consumption patterns according to their needs at different stages of their lives.
While based on an examination of individual behaviour, this theory provided important predictions for the economy as a whole. It predicts that the aggregate saving of a country is dependent on the rate of growth of national income, not its level. Also, the stock of wealth in an economy is related to the length of retirement span. Although there were initially many challenges to this theory of consumption, its relevance in economic thinking has been recently acknowledged.
The Hypothesis
Assume that there is a consumer who expects that he will live for another T years and has wealth of W. The consumer also expects to earn income Y until he retires R years from now. In this situation the consumer's resources over his lifetime consists of his initial endowment of wealth, W, and his lifetime earnings of RY. It has to be added that we are assuming that the interest rate is zero. If the interest rate was positive, we would have to account for the interest earned on savings.
The consumer can distribute his lifetime resources over the remaining T years of his life. He divides W + RY equally among T years and in each year he consumes
The consumption function of this person can be written as
If every individual in the economy plans his consumption in this manner, then the aggregate consumption function will be quite similar to the individual one. Thus, the aggregate consumption function of the economy is
where a is the marginal propensity to consume out of wealth and b is the marginal propensity to consume out of income.
Implications
From the equation given above, it is clear that if the income falls to zero the amount of consumption will be equal to aW. However, this is not a fixed value, as it depends on wealth. Moreover, according to the given consumption function, the average propensity to consume is
Since wealth does not change proportionately with income from individual to individual or from year to year, we should get the result that high income leads to a low average propensity to consume while looking at the data across persons or over short periods of time. However, generally over a long period of time, wealth and income increase together which leads to a constant ratio W⁄Y and thus a constant average propensity to consume. In order to further analyse the implications of the life-cycle model we start by considering the case of a stationary economy in which population and productivity are constant through time. Then, we relax these assumptions one by one.
Saving and Wealth when Income and Population are stable
In an unpublished paper written with R. Brumberg, it was observed that if we make some rational guesses about the average duration of working life and retired life and additionally assume that the rate of earning is constant till retirement and so is the rate of consumption combined with a zero rate of return on net worth we can find that in a stationary economy of constant population and productivity, the aggregate stock of wealth would be very significant. Moreover, under the given conditions, the aggregate rate of saving would become zero as the level of positive saving by the individuals during their earning years would be offset by the dissaving of the retired households using up their earlier accumulation. Hence, wealth will remain constant in totality even though it is constantly being transferred from dissavers to savers in exchange for current resources.
The Effect of Population Growth
Let us assume that income grows as a consequence of population growth or due to growth in income per employed which is itself a consequence of increasing productivity. We can then prove that saving will be positive even if there are no bequests. We initially analyse the effect of pure population growth while keeping all other assumptions the same. If the size of the cohorts born in successive years grows at the rate p then both population and the aggregate income will grow at the rate p. As a result of this growth there will be an increase in the ratio of younger individuals in their earning phase to retired individuals in their dissaving phase, leading to a positive net flow of saving. It can also be seen that if the rate of growth of population is constant in time then aggregate saving and wealth will also increase at the rate p and hence will be proportional to aggregate income.
The Effect of Productivity Growth
We now consider the situation where population is stationary but average income earned at each age, and hence, aggregate income rises continuously over time due to increasing productivity. This will also have a tendency to lead to a positive rate of saving and a growing stock of wealth. This is due to fact that each successive cohort will enjoy earning greater than the preceding cohorts, and thus a large level of consumption at each age, since by assumption the allocation of consumption over life remains unchanged in time. Moreover this implies that the currently working generation will aim for a level of consumption in their post-retirement years larger than the consumption enjoyed by the currently retired individuals belonging to a less affluent generation. In order to support this future level of consumption post-retirement, the working individuals will have to save currently on a scale higher than the dissaving of the retired households. Hence even if population is stationary net aggregate saving will have a tendency to be positive.
Theory and Evidence
The findings of many economists bring out a problem in the life-cycle model. It was found out that the elderly do not dissave as quickly as has been said in the model. There are two explanations for the aforementioned behaviour of the elderly.
The first explanation is that the retired individuals are cautious about unpredictable expenses. The additional saving that arises due to this behaviour is called precautionary saving. Precautionary saving may be made for the probable event of living longer than expected and hence having to provide for a longer than the planned span of retirement. Another rational reason is possibility of ill-health and huge medical expenses. These probable events make the elderly save more.
The second explanation is that the elderly may save more in order to leave bequests to their children. This will discourage dissaving at the expected rate.
Overall research on the retired section of the society show that the life-cycle model cannot completely explain consumer behaviour. Providing for retirement is an important reason for dissaving. However precautionary saving and bequests are also important.
References
- Mankiw, Gregory (5th edition). Macroeconomics.
- Angus Deaton (2005). Franco Modigliani and the Life Cycle Theory of Consumption, Research Program in Development Studies and Center for Health and Wellbeing, Princeton University.
- Modigliani, Franco, 'The Life Cycle Hypothesis of Saving, the Demand for Wealth and the Supply of Capital, Social Research, (1966:Summer). Extracted from PCI Full Text, published by ProQuest Information and Learning Company.
- Dornbusch, Fischer, Startz. Macroeconomics.